数据结构

数据结构按照逻辑结构分为线性结构/树结构/图结构

线性结构一对一
树结构一对多
图结构一对多

列表

列表(其他语言也称为数组) 数组和列表有两点不同:

数组元素类型要相同
数组长度固定

栈

数据集合只能在一端插入或删除操作的列表栈的特点:后进先出基本操作:

进栈 push
出栈 pop
取栈顶 gettop

#栈的基本实现
class Stack:
    def __init__(self):
        self.stack = []
    def push(self,element):
        self.stack.append(element)
    def pop(self):
        return self.stack.pop()
    def get_top(self):
        if len(self.stack) > 0:
            return self.stack[-1]
        else:
            return None

栈的应用 括号匹配问题 给一个字符串/其中包含小括号/中括号/大括号,求该字符串中的括号是否匹配.

队列

队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除
进行插入的一端称为队尾(rear),插入动作称为进队或入队
进行删除的一端称为队头(front),删除动作称为出队
队列的性质,先进先出(First-in,First-out)

环形队列

当队尾指针front=Maxsize-1时,再前进一个位置就自动到0

队首指针前进1:front=(front+1)%MaxSize
队尾指针前进1:rear=(rear+1)%MaxSize
队空条件:rear == front
队满条件:(rear+1)%MaxSize == front

# __*__ coding=utf-8 __*__

class Queue:
    def __init__(self,size=100):
        self.queue = [0 for _ in range(size)]
        self.size = size
        self.rear = 0
        self.front = 0

    def push(self,element):
        if not self.is_filled():
            self.rear = (self.rear + 1)%self.size
            self.queue[self.rear] = element
        else:
            raise IndexError("Queue is filled.")

    def pop(self):
        if not self.is_empty():
            self.front = (self.front + 1) % self.size
            return self.queue[self.front]

    def is_empty(self):
        return self.rear == self.front

    def is_filled(self):
        return (self.rear + 1) % self.size == self.front

q = Queue(5)
for i in range(4):
    q.push(i)
print(q.is_filled())

print(q.pop())
q.push(4)

栈和队列的应用问题迷宫问题

深度优先搜索

回溯法 思路:从一个节点开始,任意找到下一个能走的点,当找不到能走的点时,退回上一个点寻找是否有其他方向的点.

广度优先搜索思路:从一个节点开始,寻找所有接下来能继续走的点,继续不断寻找,直到找到出口.

链表

链表是由一系列节点组成的元素集合.每个节点包含两部分,数据域item和指向下一个节点的指针next.通过节点之间的相互连接,最终串联成一个链表.

class Node(object):
    def __init__(self):
        self.item = item
        self.next = None

创建链表

头插法尾插法

# __*__ coding=utf-8 __*__

class Node:
    def __init__(self,item):
        self.item = item
        self.next = None

def create_linklist(li):
    head = Node(li[0])
    for element in li[1:]:
        node = Node(element)
        node.next = head
        head = node

    return head
def print_linklist(lk):
    while lk:
        print(lk.item,end=',')
        lk = lk.next
lk = create_linklist([1,2,3])
print_linklist(lk)
print(lk.item)

链表的插入

p.next = curNode.next
curNode.next = p

链表的删除

p = curNode.next
curNode.next = curNode.next.next
del p

双链表

双链表的每个节点有两个指针:一个指向后一个节点,另一个指向前一个节点

class Node(object):
    def __init__(self):
        self.item = item
        self.next = next
        self.prior = prior

双链表的插入

p.next = curNode.next
curNode.next.prior = p
p.prior = curNode
curNode.next = p

双链表的删除

p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

链表--复杂度分析

顺序表与链表

按元素值查找
按下标查找
在某元素后插入
删除某元素

链表的插入和删除的操作明显快于顺序表链表的内存可以更灵活的分配链表这种链式存储的数据结构对树和图的结构有很大的启发性

哈希表

哈希表是一个通过哈希函数来计算数据存储位置的数据结构,通常支持操作:

insert(key,value):插入键值对(key,value)
get(key):如果存在键为key的键值对则返回其value,否则返回空值
delete(key):产出键值为key的键值对

直接寻址表当关键字的全域U比较小时,直接寻址是一种简单而有效的方法.

直接寻址表 + 哈希 = 哈希表

直接寻址表:key为k的元素放在k位置上改进直接寻址表:哈希(Hashing)

构建大小为m的寻址表T
key为k的元素放到h(k)位置上
h(k)是一个函数,其将域U映射到表T[0,1,...,m-1]

哈希冲突

开放寻址法
拉链法

字典与集合都是通过哈希表来实现的

树与二叉树

一个基于树的简单文件系统的实现

class Node:
    def __init__(self,name,type='dir'):
        self.name = name
        self.type = type
        self.children = []
        self.parent = None

    def __repr__(self):
        return self.name

class FileSystemTree:
    def __init__(self):
        self.root = Node("/")
        self.now = self.root

    def mkdir(self,name):
        #name 以 / 结尾
        if name[-1] != "/":
            name += "/"
        node = Node(name)
        self.now.children.append(node)
        node.parent = self.now

    def ls(self):
        return self.now.children

    def cd(self,name):
        if name[-1] != "/":
            name += "/"
        for child in self.now.children:
            if child.name == name:
                self.now = child
                return
        raise ValueError("invalid dir.")



tree = FileSystemTree()
tree.mkdir("var/")
tree.mkdir("bin/")
tree.mkdir("usr/")

tree.cd("bin/")
tree.mkdir("python/")

print(tree.ls())

二叉树的实现

class BiTreeNode:
    def __init__(self,data):
        self.data = data
        self.lchild = None
        self.rchild = None

a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")

e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f

root = e
print(root.lchild.rchild.data)

##二叉树的遍历

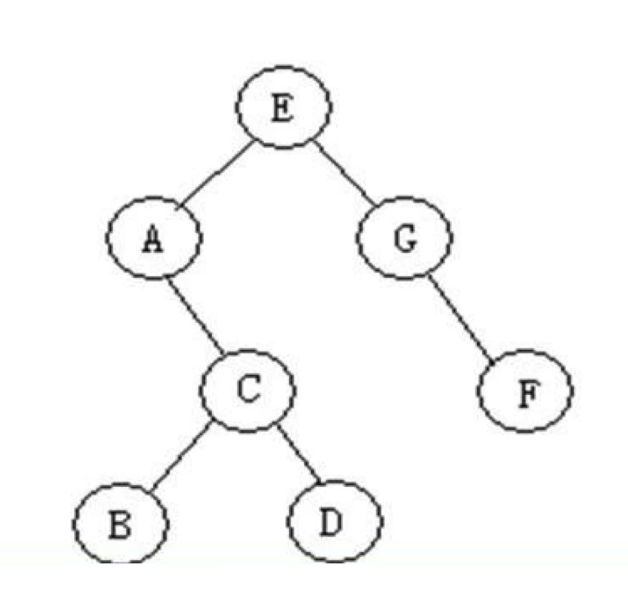
二叉树的遍历方式: 截屏2021-01-04 下午4.11.47.png

前序遍历:EACBDGF
中序遍历:ABCDEGF
后序遍历:BDCAFGE
层次遍历:EAGCFBD

#四种遍历方法的实现
def pre_order(root):
    if root:
        print(root.data,end=",")
        pre_order(root.lchild)
        pre_order(root.rchild)
#pre_order(root)

def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data,end=",")
        in_order(root.rchild)
#in_order(root)
def post_order(root):
    if root:
        post_order(root.lchild)
        post_order(root.rchild)
        print(root.data,end=",")
#post_order(root)

def level_order(root):
    queue = deque()
    queue.append(root)
    while len(queue) > 0:
        node = queue.popleft()
        print(node.data,end=",")
        if node.lchild:
            queue.append(node.lchild)
        if node.rchild:
            queue.append(node.rchild)
level_order(root)

二叉树的删除操作

如果要删除的节点是叶子节点:直接删除.
如果要删除的节点只有一个孩子,将此节点的父亲与孩子连接,然后删除该节点.
如果要删除的节点有两个孩子:将其右子树的最小节点(该节点最多有一个右孩子)删除,并替换当前节点.

    def __remove_node_1(self, node):
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:
            node.parent.lchild = None
        else:
            node.parent.rchild = None

    def __remove_node_2l(self, node):
        if not node.parent:
            self.root = node.lchild
            node.lchild.parent = None
        elif node == node.parent.lchild:
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        if not node.parent:
            self.root = node.rchild
        elif node == node.parent.lchild:
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent

二叉搜索树的效率

平均情况下,二叉搜索树进行搜索的时间复杂度为O(lgn) 最坏情况下,二叉搜索树可能非常偏斜解决方案:

随机化插入
AVL树

AVL树

AVL树是一棵自平衡的二叉搜索树 AVL树具有以下性质:

根的左右子树的高度之差的绝对值不能超过1
根的左右子树都是平衡二叉树
插入一个节点可能会破坏AVL树的平衡,可以通过旋转操作进行修正

AVL插入:

不平衡是由于对K的右孩子的右子树插入导致的 -- 左旋

不平衡是由于对K的左孩子的左子树插入导致的 -- 右旋

不平衡是由于对K的右孩子的左子树插入导致的: 右旋-左旋

不平衡是由于对K的左孩子的右子树插入导致的: 左旋-右旋

github address:

https://github.com/chenbokaix250/ForSomeForMySelf

算法2——数据结构

相关文章：